分かったようでよくわからないUUID(GUID) - なぜ重複しないの?

Abstract
Introduction
難しいことを考えず手軽にユニークなIDがほしいときに利用しがちなUUID(Universally Unique Identifier)、またはGUID(Globally Unique Identifier、マイクロソフトによるUUIDの実装)。利用する側で特にルール等を設けなくても、分散環境(直接つながっていない、依存しあっていないシステム間)であっても、世界中どこでも、まず重複することがないといわれているこのUUID、でも何で重複しないのか?どういった理屈なのか?
疑問を持ちつつも、まあみんなが重複しないといっているのだからよいか、とダメ思考になりがちでしたが。。。雨の休日、特にすることもないので調べてOutputしてみようと思います。
ざっくり結論
- UUIDはRFCで仕様が規定されていて、生成方法の違いによりいくつかのバージョンが存在する
- 今日、よく使用されるUUID バージョン4は、乱数によって生成されている
- UUID バージョン4は、128bit(16進数 32桁)中、バージョンとバリアントを示すために6bit(16進数2桁)が固定されているため実質122bitの乱数である
- 一様な(偏りのない)乱数が生成される前提であれば、122bitの乱数が重複する確率は極めて小さい
- 毎秒1億個のUUID生成を100年間繰り返して、ようやく重複する確率が50%に達する
- それ故に、現在のコンピューター環境においてはUUIDの重複はほぼ起こりえないと考えられる
- コンピューターで扱われている事象に絶対はなく、限りなく発生しない・発生させようとしたら途方もない時間がかかる状態を作り出すことによって安全性を担保している(計算量的安全性)
- UUIDの重複が絶対に発生しないと疑われるような状況になると、現在の暗号セキュリティの信頼性そのものまで疑う必要がでてくる
UUIDの概要と利用用途
UUID・GUIDは、コンピューターシステム上で、オブジェクトを一意に識別するための128bitの識別子であり、16進数で下記のように表記されます。
66775723-f019-418c-884a-787724643d06
そのユニーク性から、DBの主キーやユーザ識別子、トランザクション処理のIDといったアプリケーション層から、ファイルシステムやプロセス管理といったOS層まで幅広く活用されています。
UUIDには生成方法の違いによっていくつかのバージョンがあります。生成ハードのMACアドレスとタイムスタンプを使用したものやハッシュ関数を使用したもの、純粋に乱数のみを使用したもの等。
ここでは、今日使用頻度の高い、乱数によって生成されるバージョン4に着目していきたいと思います。
UUID バージョン4の桁数とパターン数
UUIDバージョン4は、あらかじめ固定された6bit(バージョンとバリアントを示すため)を除く122bitで構成される乱数、すなわちランダムな数字列です。ランダムな数字列というと何だか重複しそうな気がしなくもないですよね。そこで、122bitで表現可能な数字列は一体 何パターンあるのか計算してみましょう。2進数で表現可能な数字列のパターンは、
- 1bit であれば、2^1 = 2パターン(0 と 1)
- 2bit であれば、2^2 = 4パターン(00 と 01 と 10 と 11)
- 122bit は、2^122 = 1125899906842624^2 、桁が大きすぎるので近似します。
2^122 = 1125899906842624^2 ≒ (10^15)^2 = 10^30パターン
10^30とはいったいどんな桁でしょうか。参考までに
- 億:10^8
- 兆:10^12
- 京:10^16
- 垓(がい):10^20
- 澗(かん):10^24
- 正(せい):10^28
- 溝(こう):10^32
だそうです。膨大な桁のパターン数ですよね。。。このオーダーの数字が運悪く偶然重複してしまうなんて、感覚的には非常に考え辛いと思います。
UUID重複確率
では、感覚ではなく数学的に、実際に重複・衝突する確率はどんなものなのか、調べてみました。
考え方として、n回試行するとしたとき、
- 1回目:衝突対象がいないので、衝突しない確率は1(100%)
- 2回目:1回目と同じものがでれば衝突なので、1/パターン数の確率で衝突する、すなわち衝突しない確率は、1-(1/パターン数)
- 3回目:1回目と2回目ででた2つと同じものがでれば衝突なので、2/パターン数の確率で衝突する、すなわち衝突しない確率は、1-(1/パターン数)
・・・
- n回目:1回目からn-1回目と同じものがでれば衝突なので、(n-1)/パターン数の確率で衝突する、すなわち衝突しない確率は、1-((n-1)/パターン数)
となり、n回試行したときに一切衝突しない確率は、それぞれの積によって求められます。
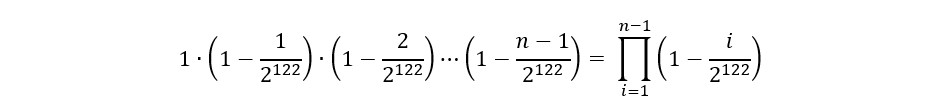
1回でも衝突が発生する確率はこの背反なので、
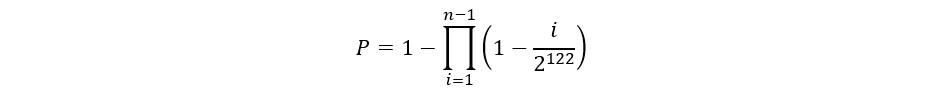
となりました。今回 パターン数は、先に述べた通り2^122なのでこうなります。
これもう少し計算しやすいよう近似すると…
(このあたりから大学での高等数学が苦手だった私にはついていけませんが)
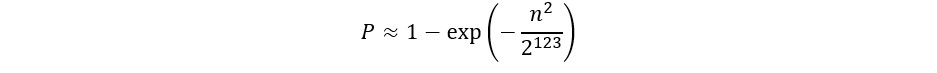
P=0.01、1%の確率で衝突を発生させようとした場合、約3*10^17回の生成、つまり京を超えるオーダーの回数繰り返して初めて1%の確率で衝突するとのことでした。やっぱり途方もない数字ですね。これだけ見てもまず重複することはないだろうと思えてきます。
もう少し詳しい数式の解説は、下記 参考文献参照。
終わりに
UUIDバージョン4は、乱数によって構成されるため、理論上の重複が絶対に発生しないとは言えないものの、122bitの乱数の膨大な組み合わせの上に成り立っていることから、事実上 重複することが起こりえないといえるでしょう。重複確率を1%にするのでさえ京を超えるオーダーの回数試行する必要があり、別の視点でみると毎秒1億個のUUID生成を100年間繰り返して、ようやく重複する確率が50%に達するとか。
ただしこれは発生させる乱数に偏りがないこと(一様であること)が前提となります。乱数に偏りがありどこかによく発生する領域があるようだと、重複は起こりやすくなってしまいます。この前提は、コンピューター上で一様な疑似乱数をいかに発生させるかという別のテーマになるので、ここでは割愛させていただきます(気が向いたらまた取り上げるかも)。
現代のコンピューターシステムでは、このように理論上 絶対ではないが、現実にはまず発生しない、発生させようとしたら途方もない時間がかかる状態を作り上げることによって、「発生しない」とみなす考え方が広く取り入れられています。
このような考え方は計算量的安全性と呼ばれ、現代の暗号セキュリティもこれに則り構築されています。数学的には暗号は必ず解読(復号)できる、等式の左辺(暗号化する前の平文)から右辺(暗号文)が作られている以上は、必ず右辺(暗号文)から左辺(暗号化する前の平文)は求めることができる。ただし右辺(暗号文)から左辺(暗号化する前の平文)を求めるにはtry and errorを繰り返す必要があり、そこにかかる試行回数・時間が途方もないものであるが故に、現実的は誰も解読できないという理屈で成り立っています。
よって、UUIDの重複を疑い始めてしまうと、現代の暗号セキュリティも信用できなくなり、現代社会が成立しません。でも現実はそうでないですよね、故にUUIDが重複することも現実的には起こりえないということになるでしょう(かなり乱暴な論理)。
参考文献
Comments